精密制造与自动化
2016年第2期
基于LOR最优调节器的平面二级倒立摆的
建模与仿真姜岩蕾史增芳
(河南工业职业技术学院河南南阳473000)
摘要倒立摆控制系统是一个典型的高阶次、不稳定、多变量、非线性和强耦合控制系统。通过研究分析平面二级倒立摆控制系统的数学模型，用线性二次型最优调节器（LQR），实现对二级倒立摆的最优控制，MATLAB 仿真结果表明了该方法的有效性。
关键词最优控制器倒立摆最优控制
倒立摆是理想的自动控制教学实验设备，它能
全方位地满足自动控制教学的要求。许多抽象的控制概念如系统稳定性、可控性、系统收敛速度和系统抗干扰能力等，都可以通过倒立摆直观地表现出来目。由于倒立摆系统的高阶次、严重不稳定、多变量、非线性和强耦合等特性，吸引着许多学者和研究人员不断地从倒立摆控制中发掘新的控制策略和算法，文献[2]、[3]提出了基于模糊神经网络的倒立摆控制系统，该方法有效地克服了系统存在的非线性和不确定性，但该方法过分依赖人类直接控制被控对象的经验。文献[4]、[5]提出了倒立摆拟人控制方法，系统的稳定范围大，鲁棒性好，但控制率从定性到定量的转化较复杂。本文采用基于状态空间设计法的LQR最优调节器，较好地兼顾了系统的鲁棒稳定性和快速性。MATLAB仿真结果表明了该方法的有效性。
1倒立摆系统数学建模及仿真
倒立摆系统最终的控制目的是使倒立摆这样一
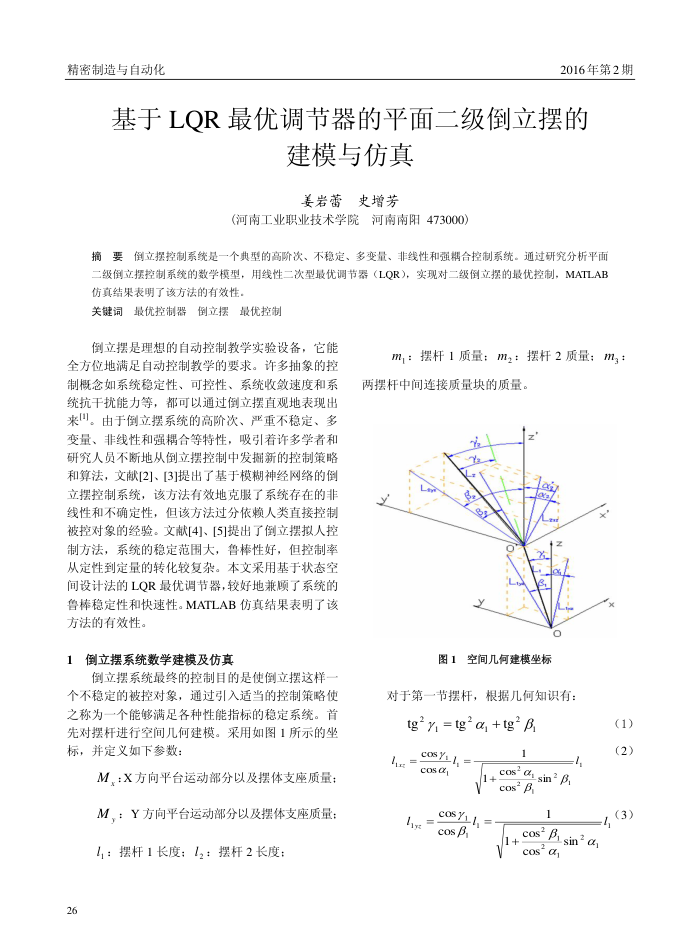
个不稳定的被控对象，通过引入适当的控制策略使之称为一个能够满足各种性能指标的稳定系统。首先对摆杆进行空间几何建模。采用如图1所示的坐标，并定义如下参数：
M，：X方向平台运动部分以及摆体支座质量： M、：Y方向平台运动部分以及摆体支座质量 1，：摆杆1长度：，：摆杆2长度：
26
m,：摆杆1质量：mz：摆杆2质量；m,: 两摆杆中间连接质量块的质量。
图1空间几何建模坐标
对于第一节摆杆，根据几何知识有：
tg" = tg’ α, + tg β,
cosyL cosα
cosyl cosβ,
-
.coch sin B. cos"p,
1
Ji+cos*Basin'a cosa,
(1)(2)
(3)