数控技术
基于现代控制理论的电机应用实例
杨墨
(东南大学江苏南京210008)
摘要本文介绍了加何给小型直流电机设计完整的住置控制系统采用现代控制理论械点配置的控制方法，应用Matlab/Simulink软件对控制系统进行辅助分新和设计,并运用Simulink实时控制功能设计控制器,使系统满足给定的性能指标。
关键词：控制系统控制原理
中图分类号：TP273
文缺标识码：A
文章露号:10079416(2013)06003402
现代控制理论是建立在状态空间法基础上的一种控制理论，对控制系统的分析和设计主要是通过状态变量来进行。与经典控制理论相比，其所能处理的控制间题要更加广泛，包括线性系统和非线性系统，定常系统和时变系统，单变量系统和多变量系统，所采用的算法也更适合于在数字计算机上进行。
本论文通过为小型直流电机机组设计完整的位置控制系统，采用现代控制理论状态反馈和状态观测的原理。功能强大的Matlab/ Simulink软件，在对控制系统进行分析和设计时发挥着重要的作用， Simulink可与硬件设备实现实时控制的功能，最终，使得整个系统能够满足给定的性能指标(无静态误差，电机响应时间<0.3s，超调量<20%)。 1主要控制原理
1.1状态反馈原理
用全状态反馈实现二阶系统极点的任意配置，其动态性能一定会优于只有输出反馈的系统。设受控对象的动态方程为
+X = X
=
令u=F-Kx,其中K=[K，k，..k,]，r为系统的给定量，x 为nx1系统状态变量，u为1x1控制量。则引人状态反馈后系统的状态方程变为：=(4-bK)x+bur，相应的特征多项式为： det[SI-(4-bK]]，调节状态反馈阵k的元素[K，k，.k,],就能实现闭环系统极点的任意配置，如图1所示：
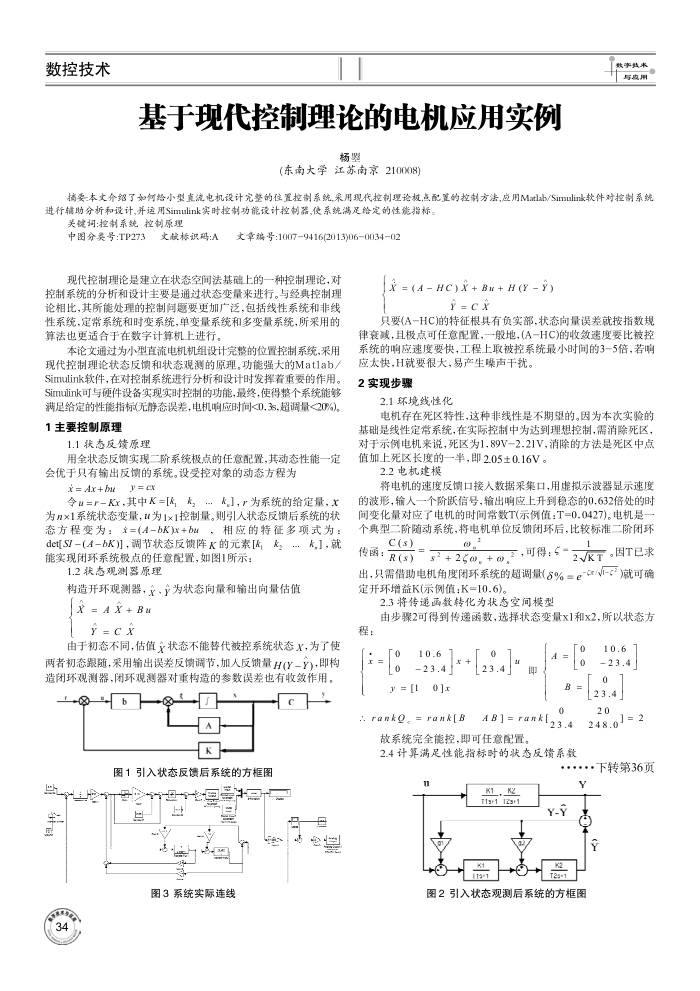
1.2状态观测器原理
构造开环观测器，、为状态向量和输出向量估值
X=4X+Bu Y=cx
由于初态不同，估值文状态不能替代被控系统状态X，为了使两者初态跟随，采用输出误差反馈调节，加人反馈量H(Y-).即构造闭环观测器，闭环观测器对重构造的参数误差也有收效作用。
8 e
b
区
A
图1引入状态反馈后系统的方框图
国
图3系统实际连线
c
中
X = (4 - HC) X + BH + H (Y Y)
y=cx
只要(A-HC)的特征根具有负实部，状态向量误差就按指数规律衰减，且极点可任意配置，一般地，(A-HC)的收效速度要比被控系统的响应速度要快，工程上取被控系统最小时间的3-5倍，若响
应太快，H就要很大，易产生噪声干扰。 2实现步骤
2.1环境线性化
电机存在死区特性，这种非线性是不期望的。因为本次实验的基础是线性定常系统，在实际控制中为达到理想控制，需消除死区，对于示例电机来说，死区为1.89V-2.21V，消除的方法是死区中点值加上死区长度的一率，即2.05±0.16V。
2.2电机建模
将电机的速度反馈口接人数据采集口，用虚拟示波器显示速度的波形，输人一个阶跃信号，输出响应上升到稳态的0.632倍处的时间变化量对应了电机的时闻常数T(示例值：T=0.0427)。电机是个典型二阶随动系统，将电机单位反馈闭环后，比较标准二阶闭环
c(s)
0.1
传函：R(8)
2VKT。因T已求
二，可得：。
$2 + 260, + o,2
出，只需借助电机角度闭环系统的超调量（5%=e"c/V-c")就可确定开环增益K(示例值：K=10.6)。
23将传递函数转化为状态空问模型
由步骤2可得到传递函数，选择状态变量x1和x2，所以状态方程：
10.6 23.4
y= [1
0]x
.rankO,= rank[B
23.4
4 B
Fo
0
AB] = rank[23.4
故系统完全能控，即可任意配置。
2.4计算满足性能指标时的状态反馈系数
10.6 23.4
0
23.4
20
248.0J=2
.下转第36页
K1K2 T15+1 123+1
Y-Y
Y
图2引入状态观测后系统的方框图