应用研究
粒子滤波在GPS/DR组合导航中的应用
周福涛任波
(沈阳理工大学装备工程学院辽宁沈阳110159)
摘要：粒子滤波算法作为一种基于蒙特卡罗方法的遗推贝叶斯估计，适用于非线性非高斯系就的分析，被广逐应用于跟踪、定位等问题的研究中。本文详细介绍了粒子滤波的基本原理并给出了粒子滤波在GPS/DR组合导航中的一个应用实例。
关键调：GPS/DR组合导航粒子滤波
中图分类号：TN713
文献标识码：A
文章编号：1007-9416(2011)08-0064-02
传统的卡尔受滤波理论只适用于线性系统，要求系统模型准确，噪声为已知高斯过程，是一种线性最小方差估计。现实中非线性滤波问题是极为普遍的，卡尔叠滤波对于非线性系统并不适用在非线性系统中应用最广泛的是扩展卡尔受滤波(EKF)，EKF的基本思想是将非线性模型线性化，然后再进行卡尔滤波。EKF实现简单，但由于线性化过程中会引起误差，导致估计精度下降，粒子滤
波适用于强非线性，非高斯噪声系统模型的滤波。 1、GPS/DR组合导航模型
取GPS/DR组合导航系统的状态向量为X=[x)V” a)，Va)，其中)Ve分别为车辆在k时的东向位置速度和加速度，)Vt)，α()分别为k时刻的北向位置、速度和加速度，采用机体载体的当前"统计模型来描述车辆加速度的统计分布，则系统的状态方程(参考文献")为：
X, = @++--X+-+ +W--
其中W-为系统噪声向量，Φ，-为一步状态转移矩阵，
T2 2
@
0 0
00 0
0
0
o 0
0 0 0 r 2
将GPS输出的东向位置信息e，北向位置信息O，角速率陀螺的输出w以及里程计在一个采样周期内输出的距离s为观测量，则系统的离散观测方程为：
xeca Xa
Z
Ve(a)det) Vele)da(t)
Vea) + Vaa) T yvan +Vat
Vun Va
e)
其中，Va)6、6》为观测噪声，分别近似为(0,0）(0,α)、(0,α）、(0,)的高斯白噪声，可以看出系统的观测方程为非线性的。
2、粒子滤波算法
粒子滤波以蒙特卡罗方法和贝叶斯理论为基础，粒子滤波基本思想是首先根据系统状态向量的经验条件分布，在状态空间中产生一组随机样本集合，然后根据观测量不断地调整致子的权重和位置，通过调整后的粒子信息，修正最初的经验条件分布，即粒子滤波利用状态空间中的随机样本对状态的后验概率密度进行近似。若 P(xzu)为一后验概率密度函数，(i=1,2-N)为N个来自后验概
64 方游数据
率密度函数px%)的独立同分布的随机变量，则后验概率密度函数可表示为：P(|zu-)6(-对)式中，w为相应粒子的权重，这样就将贝叶斯估计中的积分问题转换为和运算的间题。然而后验概率密度函数一般为多维非标准函数，直接从后验概率密度抽样比较困难。这时就需要一个容易从中进行采样的密度函数，即重要性概率密度函数。通常的做法是选取先验概率密度为重要性密度函数，即n(x,x,--y,)=p(x,x,-)则相应的权重可表示为w=w-P(x,Ix-)由此可得到基于序列重要性采样(SIS)的基本粒子港波算法，其典型SIS算法步骤如下；
(1)从g(x,1xa-z,)中随机抽取n个有限样本(2)逐点计算对应的p(x-1zt-)和p(z,1,)
(3)利用权值公式计算对应样本的重要性权系数(4)对权进行归一化处理
w
w w
(5)对p（x，1zr）进行估计
序列重要性采样(SIS)算法存在的个基本间题就是退化现象，即经过几步选代递推后，许多粒子的权重变得非常小，大量的计算则浪费在小权值粒子上毫无意义。退化现象的程度可以由有效粒子数来衡量，有效粒子数定义如下，
N
减少粒子退化现象一个最直接的方法就是增加采样的粒子数，
15 10
单位m
位置误差
5 10
100
200
300
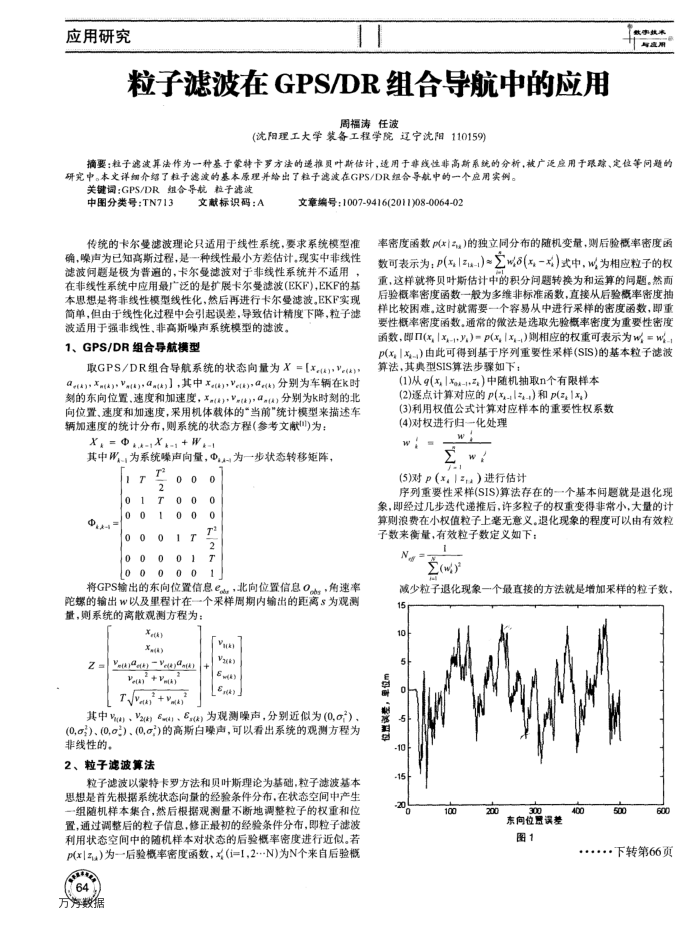
东向位置误差图1
400
500
600
下转第66页