数事载本与率用
算法分析
PSO-BP算法优化PID控制在光照系统中的应用
王需
(公安海警学院浙江宁波315801)
摘要:本文主要采用粒子群算法去优化基于BP神经网络整定的PID控制算法，令PID控制算法的收效更加迅速,推索能力更强,最终使得PID控制系统的控制效果更加理想,在使用粒子群算法(PSO)对BP神经网络加以改进后,能令新的PSO-BP网络比普通的BP网络具有更强的提素能力,应用到PID控制光熙系统中效果更好
关键词:PID控制BP神经网络轻子群优化算法PSO-BP算法
中图分类号：TP273
文献标识码：A
PSO算法是近年流行的一种智能优化算法，将PSO算法与BP神经网络算法相结合可以有效的解决BP神经网络自身存在的缺陷，利用粒子群算法来代替BP网络中梯度下降法，从而可以更好地优化 BP网络各层间的连接权值，进而提高了BP神经网络的泛化能力、学习能力，并且大大提升它的收效速度
而粒子群算法优化BP神经网络的过程主要是利用粒子群的送代来代替BP神经网络算法中的梯度修正，利用PSO算法来优化BP神经网络的权值训练，用PSO算法解决BP神经网络中的问题，关键要做到以下两点：
(1)粒子群算法中粒子的维度数值与BP神经网络中的连接权值的数量相对应。将PSO中的每一个粒子的维度分量对应的作为BP神经网络中的每一个连接权值。PSO算法中的关键在于粒子，众多粒子构成了一个多维的向量，而连接权值的个数与粒子的维数保持一致，
(2)将粒子群算法的适应函数用BP神经网络中的均方误差函数回来替代，同时利用粒子群算法强大的送代搜索能力使得BP网络的
最优个体适应良量
25
进化次数
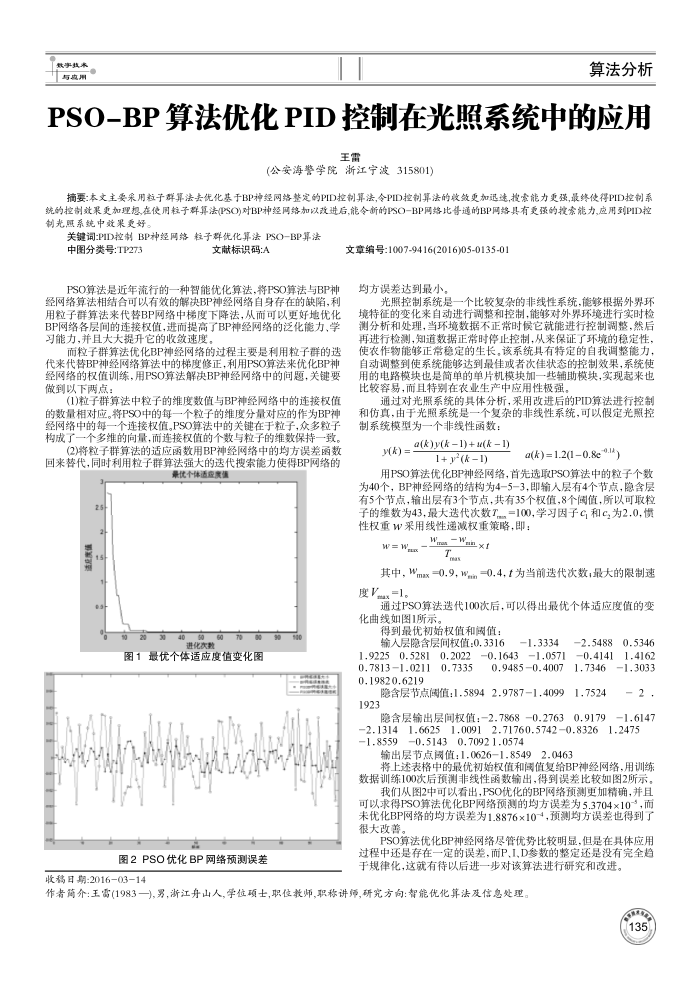
图1最优个体适应度值变化图图2PSO优化BP网络预测误差
收稿日期：201603-14
文章编号:1007-9416(2016)05-0135-01 均方误差达到最小。
光照控制系统是一个比较复杂的非线性系统，能够根据外界环境特征的变化来自动进行调整和控制，能够对外界环境进行实时检测分析和处理，当环境数据不正常时候它就能进行控制调整，然后再进行检测，知道数据正常时停止控制，从来保证了环境的稳定性，使农作物能够正常稳定的生长，该系统具有特定的自我调整能力，自动调整到使系统能够达到最佳或者次佳状态的控制效果，系统使用的电路模块也是简单的单片机模块加一些辅助模块，实现起来也比较容易，而且特别在农业生产中应用性极强。
通过对光照系统的具体分析，采用改进后的PID算法进行控制和仿真，由于光照系统是二个复杂的非线性系统，可以假定光照控制系统模型为一个非线性函数：
α(k)y(K 1)+ (K 1)
(k) :
1 + μ2(K 1)
α(k) = 1.2(10.8c-0.
用PSO算法优化BP神经网络，首先选取PSO算法中的粒子个数为40个，BP神经网络的结构为4-5-3，即输人层有4个节点，隐含层有5个节点，输出层有3个节点，共有35个权值，8个阔值，所以可取粒子的维数为43.最大送代次数T=100,学习因子c和c,为2.0.惯性权重W采用线性递减权重策略，即：
Wrm Waim. ×
w=w
T
其中，wmx=0.9，w=0.4，t为当前选代次数，最大的限制速度V=1
通过PSO算法送代100次后，可以得出最优个体适应度值的变化曲线如图1所示。
得到最优初始权值和阅值：输人层隐含层间权值：0.3316
1.9225 0.5281 0.2022
1.3334
0.16431.0571
0.78131.0211
0.7335
0.94850.4007
0.1982 0.6219
2.5488
0.5346
0.4141
1.4162
1.7346
1.3033
隐含层节点阔值：1.58942.9787-1.4099
1.7524
1923
隐含层输出层闻权值：-2.7868-0.2763
0.9179
2.13141.6625"1.00912.71760.57420.8326
-2, 1.6147
1.2475
1.85590.51430.7092 1.0574
输出层节点阅值：1.0626-1.85492.0463
将上述表格中的最优初始权值和阅值复给BP神经网络，用训练数据训练100次后预测非线性函数输出，得到误差比较如图2所示。
我们从图2中可以看出，PSO优化的BP网络预测更加精确，并且可以求得PSO算法优化BP网络预测的均方误差为5.3704×10~，而未优化BP网络的均方误差为1.8876×10-4，预测均方误差也得到了很大改善。
PSO算法优化BP神经网络尽管优势比较明显，但是在具体应用过程中还是存在一定的误差，而P、I,D参数的整定还是没有完全趋于规律化，这就有待以后进一步对该算法进行研究和改进。
作者简介：王雷(1983一)，男，渐江舟山人，学位颈士，职位教师，职称讲师，研究方向：智能优化算法及信息处理。
135